在工程技术研究中,很多工程计算问题可以直接或间接地归结为求解线性代数方程组,它的一般形式如下:
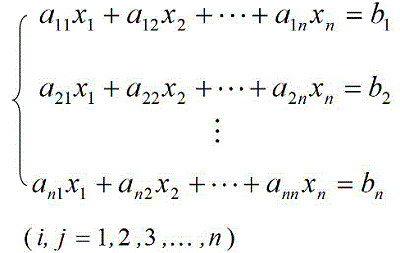
用矩阵形式表示为:Ax=b。
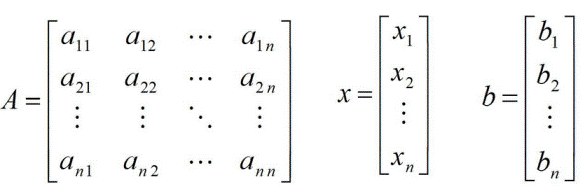
线性方程组的常用解法有:
1)直接解法:高斯消去法、列主元高斯消去法、约当消去法、三角分解法;
2)迭代解法:雅可比迭代、高斯-赛德尔迭代、超松弛迭代等解法。
对于阶数较小(n<1000)的线性方程组,直接法的准确性和可靠性要比迭代法高,因此推荐采用直接解法,最常用的为高斯消去法。
对于阶数较高的方程组,直接法计算占用的内存较大和程序的复杂性较高,因此推荐采用迭代解法,常用的有高斯-赛德尔迭代法和超松弛迭代法。迭代解法的缺点的是,可能无法收敛而求不出解,其可靠性稍差。
对于普通工程技术研究来说,高斯消去法已经完全够用,可以认为是最好的数值解法。
参考文献:
[1]何暑廷. 结构计算中线性方程组求解综述[J]. 工业技术经济,1996,06:101-102.
[2]刘进山,李小平. MATLAB平台上几种线性方程组解法的比较[J]. 科技信息(学术研究),2007,19:29-31.
X
搜索