弦截法(适用于一元非线性方程的求根问题)的提出,主要是针对牛顿迭代法不适用于f(x)求导比较复杂的情况,弦截法用差商来代替牛顿迭代法中的f’(x)。其迭代公式如下:
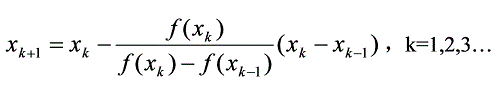
弦截法的基本步骤如下:


#include<stdio.h>
#include <math.h>
#define eps 0.00001 /* 容许误差*/
#define N 1000 /* 最大迭代次数N */
float f(float x) /* 定义函数f(x) */
{
return pow(x,3)+2*x+40-exp(x);
}
main()
{
float x0,x1,x2;
int i;
printf("input x0, x1=\n");/*注意两个数字间用空格隔开,如:"5 10"+回车*/
scanf("%f%f",&x0,&x1);
for(i=1;i<=N;i++)
{
x2=x1-(f(x1)*(x1-x0))/(f(x1)-f(x0)); /* 弦截法迭代公式*/
if(fabs(x2-x1)<eps && fabs(f(x2))<eps) /*满足精度要求输出近似根并退出*/
{
printf("Root of equation:%f, NO.=%d\n",x2,i);
system("pause");
return;
}
x0=x1; /* 准备下一次迭代的初值*/
x1=x2;
}
printf("After %d repeats, no root was solved.\n",N); /* 输出无解信息*/
system("pause");
}
弦截法与牛顿迭代法都是线性化方法,虽然二者在迭代公式的形式上类似,但它们有本质区别。弦截法比牛顿迭代法收敛速度要稍慢。
参考资料:
[1] 王汉青. 暖通空调流体流动数值计算方法与应用[M]. 北京: 科学出版社, 2013.10.
搜索